Math
Elliptic Curve
Spline
History
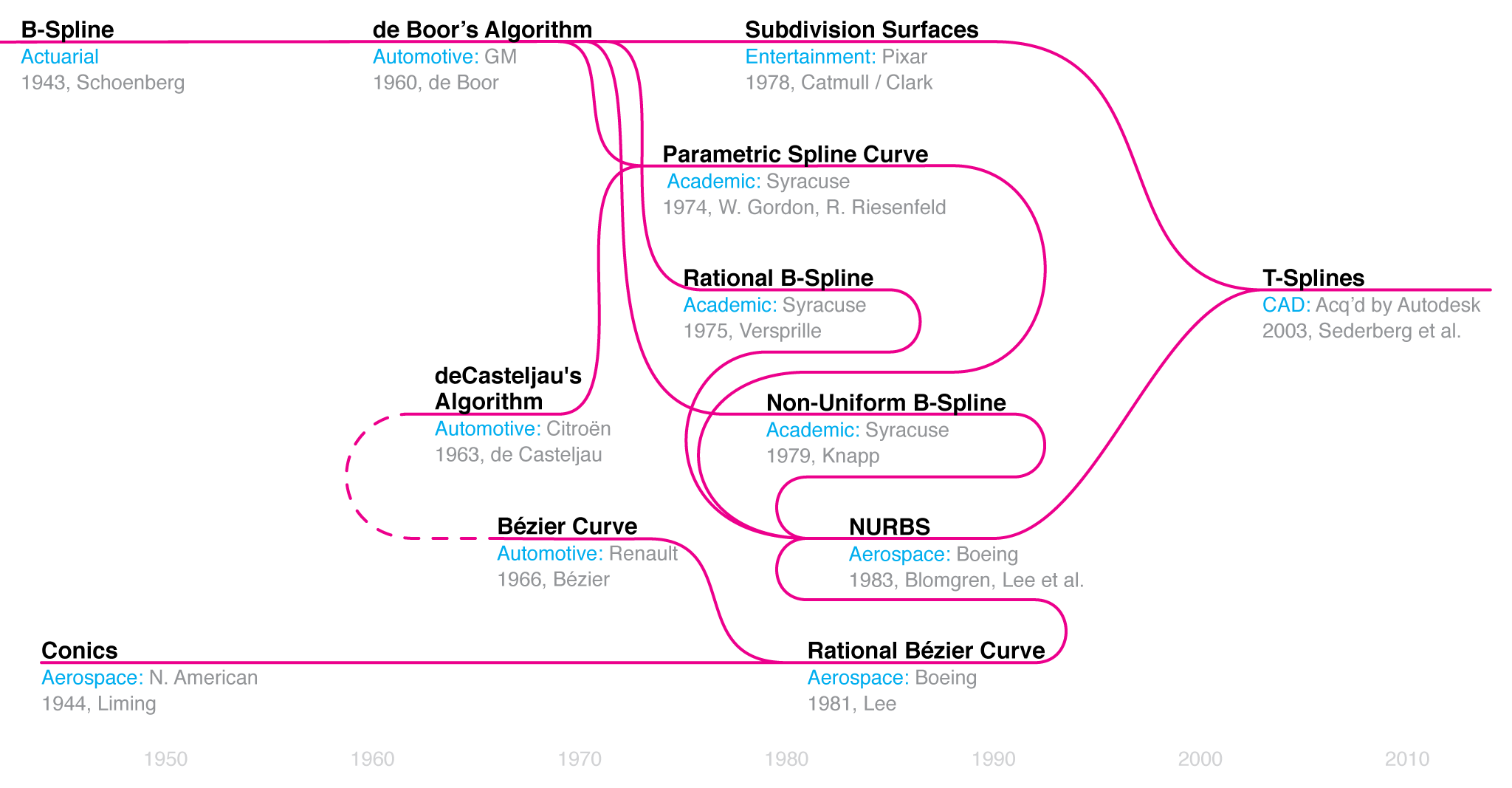
Spline 是曲線的一種,一開始是作為造船工具而使用, 設計師需要方法來畫出滑順的曲線通過一群點, 做法是在控制點上擺放金屬 (Weights), 彎曲一片薄金屬通過先前擺上的金屬 Knots,這片薄金屬彎曲形成的曲線就稱為 Spline, 而 Spline 在現今的使用中幾乎可以說是 Computational Curve 的同義詞。

knots : 節點
weight : 權重
control points : 控制點
de Boor’s Algorithm
計算 B-Spline 的演算法
deCastelijau’s Algorithm
計算 Bézier 曲線的演算法
Rational B-Spline
B-Spline 中的控制點的參數 (weight) 可以不一樣
Non-Uniform B-Spline
Uniform 是 knots 的值會慢慢規律地上升 (0, 1, 2, 3, 4, …), Non-Uniform 則是 knots 的值會慢慢不規律地上升 (0, 0, 0, 1, 2, 2, 3…)
Non-Uniform Rational B-Spline (NURBS)
T-Spline
T-Spline 是由 T-Spline 公司開發的建模技術,T-Spline 為 NURBS 的一種變種, 大幅減少 NURBS 繪製時的計算, 後來 T-Spline 公司由 Autodesk 收購。