演算法與資料結構 

介紹 

演算法與資料結構是資訊領域中非常重要的一塊，好的演算法可以節省時間和資源，但是演算法何其多，這邊只斷斷續續紀錄些許東西，另外繁體中文資料中最齊全的網站應該屬「演算法筆記」莫屬，可以多加利用。

Spatial Data Partitioning Trees 

Probabilistic Data Structures 

Probabilistic Data Structures 的特點在於告訴你「可能的」狀態，不是確切的狀況，適用於資料量大且計算不需要非常精確的狀況，可以節省資源和時間。

參考：

Bloom Filter 

Bloom Filter 的用途在測試一個值是否在一個集合內，會有 False Positive（也就是不在集合內，卻回報有在集合內），但是不會有 False Negaative（也就是是回報沒有在集合內，就真的不在集合內）， False Positive 的程度會受到使用的記憶體量和 Hash 方法影響，使用越多的記憶體可以降低 False Positive。

Bloom Filter 為 m bits 的 array，全部都初始化為 0，另外搭配 k 個 Hash 函式（k 比 m 小很多）。

Bloom Filter 支援兩種操作：

新增數值：數值經過 k 個 Hash 函式處理後取得 array index，把值標為 1
檢驗數值：數值經過 k 個 Hash 函式處理後取得 array index，如果 array 內的值為 0，則該數值真的不在這個集合中，如果 array 內的值為 1，則該數值「可能」在這個集合中

（簡單來說 Bloom Filter 就是 hash + bits vector，collision 也沒關係）

Bloom Filter 的 False Positive Rate：

../_images/bloom-filter-false-positive-rate.svg

特性：

少量的記憶體可以代表大量的數值，但是 False Positive 會上升
聯集和交集可以 Bitwise OR 和 Bitwise AND 實做

使用案例：

數個資料庫用於減少為了不存在的資料去存取硬碟（例如 Google BigTable、Apache HBase、Apache Cassandra、PostgreSQL）
Akamai 發現該公司的 web server 有將近 3/4 的 request 是一次性的，所以利用 Bloom Filter 來檢驗，當 request 重複出現時才存到 cache，可以減少硬碟 loading 和增加 cache 的 hit rate
Google Chrome 用於偵測可能有害的網站 URL
Squid 用於 Cache
Bitcon 用於加速同步
Medium 用於避免推薦使用者已經讀過的文章

參考：

Linear Counting (LC)

空間複雜度：

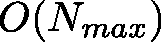
在 1990 年的一篇論文「A Linear-Time Probabilistic Counting Algorithm for Database Applications [whang1990linear] 」中被提出，屬於早期的 Cardinality Estimation 演算法，也因此空間複雜不不如後面出現的演算法來的好。

Linear Couting 會有一個 bit vector 和 Hash 函式， bit vector 一開始會初始化為 0，資料在經過 Hash 後會變成 bit vector index，此時把對應的位置標為 1，把所有資料處理過後就可以概略估計資料內不同數值的數量。

估計公式為：

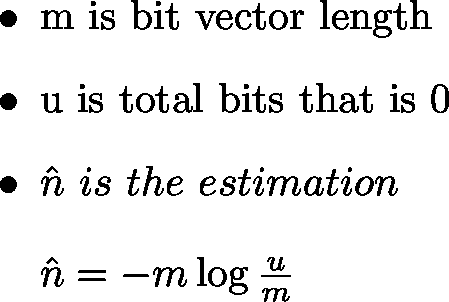
../_images/linear-counting-estimation.png

LogLog Counting (LLC)

空間複雜度：

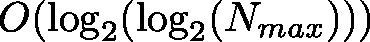
「Loglog Counting of Large Cardinalities [durand2003loglog] 」

HyperLogLog Counting (HLLC)

空間複雜度：

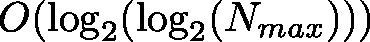
「Hyperloglog: The analysis of a near-optimal cardinality estimation algorithm [flajolet2007hyperloglog] 」

HyperLogLog 是一種解 Cardinality Estimation Problem（或稱 Count-distinct Problem）的演算法，用於概略估算集合中不同數值的數量。由於計算正確的數量需要比較多的資源與時間，尤其對於資料量大時尤其明顯，但我們在一些情況下可能可以接受誤差，於是就有了 HyperLogLog 這類演算法， HyperLogLog 更改自更早期的 LogLog 演算法，改善其不同數值的數量少的時候會有大誤差的問題，可以用極少量的記憶體來估算極大量的集合中不同數值的數量，使用 1.5 KB 的記憶體就可以估算 10 億筆資料（誤差為 2%）。

在講 HyperLogLog 前有一個重要的性質要先知道，假設資料是連續均勻分佈的（Uniform Distribution），在這個條件下已經有人觀察到可以用數值的二元表示中最多連續的 0 作為估計來源，例如這一大筆資料中最多連續的 0 是 n，則估計有 2^n 個不同的資料。

HyperLogLog 會對集合內的元素進行 Hash，藉此取得均勻分佈的資料，再套用上面提到的性質做計算，為了降低誤差， HyperLogLog 還會把資料切割成數個子集合，由子集合進行計算，最後再取調和平均數（Harmonic Mean）算出整體的結果。

想法如下，假設我們有四個 bits，則總共有 16 種可能，其中：

連續四個 0 的有一種：0000
連續三個 0 的有兩種：0001、1000
連續二個 0 的有五種：0011、1001、1100、0100、0010
連續一個 0 的有七種：0111、1011、1101、1110、0101、1010、0110
沒有0 的有一種：1111

假設我們最高連續次數為三個，則其出現的機率為 2/16，加上我們的資料是平均分佈的（或使用結果平均分佈的 Hash 函式），所以就猜我們可能有 8 筆不同的資料。

為了降低單一估計可能會有極大的偏差（Bias），可以把做分割後再取平均來降低，例如準備特定長度的 bucket vector，取資料的前 4 個 bits 作為 bucket index（所以各 bucket 的分佈狀況應該偏向平均），計算剩下資料的連續 0 數量，存入對應的 bucket 位置，最後使用 Harmonic Mean 計算平均以降低極端值（Outlier）的影響。

HyperLogLog 的標準差為 1.04 / sqrt(m) ，其中 m 為使用的 bucket vector 大小。

實際應用：