演算法相關概念

演算法分析

分析不同的演算法來衡量適用性。

複雜度

理論

理論上在討論演算法的複雜度時會使用 Big O Notation， 這種作法雖然跟實際的執行效率有差異， 但是可以大概了解演算法效率成長的狀況。

實際

演算法實際上的效率會受到實做者、實做的程式語言、執行的機器等因素影響， 而且就連一般四則運算的執行效率可能都不相同， 要實做出實際上跑起來效率好的演算法需要考慮很多東西， 例如 Cache Miss、Branch Prediction、SIMD 等。 （也因此理論的討論才把這些難以量化的因素去除掉）

Amortize Analysis

Amortize Analysis 看的是攤平的時間複雜度， 因為以 Worst Case 來看可能會過於悲觀， 造成衡量的結果更實際上有差距， 例如 Vector 的插入會在空間不夠時要更大的空間並把資料移過去， 這個操作最壞的狀況會是 O(n)， 但是最好的狀況是 O(1)， 而且大部分的狀況是 O(1)， 因此插入 n 個資料的複雜度仍是 O(n)， 平均下來就可以發現 Amortize 後仍是 O(1)。

Online 演算法通常使用 Amortize Analysis 來衡量， 不然分析出來的狀況會跟實際差太多。

Smooth Analysis

Smooth Analysis 是 Worst 和 Average 分析的混合， 目的是要有效地辨別出 Simplex這種 Worst 為指數時間卻在實際使用上很有效率的演算法， 其分析方式是以介於 Worst 和 Average 之間的資料作為輸入。 這作法的設想是現實狀況的資料不會完全混亂到變成最差的結果， 但是仍然存在著混亂性， 因此取一個不會太亂但又不會太整齊的案例作為分析對象， 藉此來衡量演算法實際上的執行效率。

如果一個演算法在 Smooth Analysis 下的複雜度不高， 那它實務上花費很長時間來解決問題的機會就不大。

這個分析方式在 2001 年被發明， 目前已經被用於數值分析、機器學習、資料探勘等領域。

演算法設計

製造適合的演算法來解決所碰到的問題。

開發步驟：

  • 定義要解決的問題

  • 定義解決問題的演算法需要哪些功能

  • 設計演算法

  • 檢查演算法的正確性

  • 分析演算法

  • 實做演算法

  • 測試實做的正確性

  • 撰寫文件

Brute Force

直接暴力的爬過所有可能來找出最佳解。

Divide and Conquer

把問題切割成數個小問題來解決。

Dynamic Programming

為 Divide and Conquer 的延伸， 在其之上加上了 Memorization， 藉此節省不必要的重複計算。

例如在計算費波那契數列時， 把先前計算的子問題答案記起來， 拿來算出下一個值， 減少計算量。

from functools import lru_cache

# using a cache to implement a dynamic programming technique
@lru_cache(maxsize=None)
def fib(n):
    if n == 1:
        return 1
    elif n == 2:
        return 2
    else:
        return f(n-1) + f(n-2)

Greedy

不斷選擇目前可見選項中看起來最好的， 藉此嘗試逼近最佳解， 但不保證得到的答案就真的是最佳解。

Backtracking

尋找所有解法的技巧， 不斷地產生出新的候選答案， 並在發現不會是解答時盡早刪除。

Design Pattern

演算法的實做上可能會利用到一些 Design Pattern 來定義界面。

演算法種類

Offline vs Online

Offline 指的是演算法需要把所有資料都讀入後才能開始運作， 例如 Bubble Sort。

而 Online 則是資料在讀取的當中就可以開始處理， 甚至可以提供目前處理的結果， 例如 Insertion Sort。

Static vs Dynamic

Static 指的是無法隨時更動原本輸入的資料（包含修改、新增、刪除）， 也無法隨時查詢目前的結果， 例如 Dijkstra’s Algorithm。

Dynamic 指的是可以隨時更動原本輸入的資料， 也可以隨時查詢目前的結果， 例如 Binary Search Tree。

Exact vs Approximation

Exact 指的是算出來的結果絕對正確。

Approximation 指的是算出來的結果會有誤差， 但是有些問題為了在有限的時間內取得答案或是為了提昇效率， 而可以接受些許的誤差。

P 和 NP 問題

P 指的是 Polynomial Time 的 P， 代表 Turing Machine 可以在多項式時間內解出來的問題。

NP 指的是 Nondeterministic Polynomial Time， 代表 Turing Machine 不能在多項式時間內解出來的問題 （例如 Exponential Time）， 而每個 NP 問題都可以經由一個多項式時間的演算法轉換成另一個 NP 問題。

NP-Completeness 是指 NP 問題中的一個子集合， 在這集合內的任意問題都可以代表整個 NP 集合（所以稱為 Completeness）， 只要解決其中任意的問題就可以解決 NP 內的所有問題， 雖然目前 NP-Completeness 問題無法在多項式時間內解出來， 但是實務上還是常碰到這種問題， 因此經常使用 Heuristic、逼近、隨機、加限制、參數化等手法來在有限時間內取得夠好的答案。

P 和 NP 問題就是指 P 集合和 NP 集合是否相等的問題， 如果 P 等於 NP 的話， 代表 NP 問題可以被轉換成 P 問題， 在多項式時間內解出來。

NP-Hard 指的是「至少」和 NP 問題一樣難的問題， 所以可能比 NP 問題來的難， 又或者等同於 NP 問題中已被證為最棘手的 NP-Completeness 一樣難。

可能的集合圖：

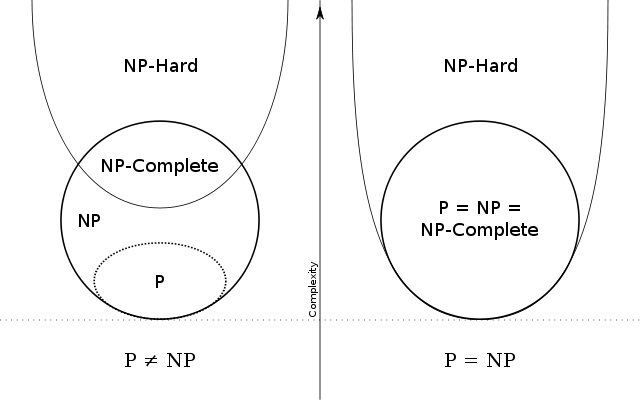
../_images/p-and-np.png

NP-Completeness 問題範例：

  • Boolean Satisfiability Problem

  • Knapsack Problem

  • Travelling Salesman Problem

  • Graph Coloring Problem

注意的是， 在 P 內的問題不代表這問題很容易解決， 因為雖然找出最佳解的時間複雜度是多項式的， 但是其多項式的係數或指數可能非常大。 反之一個 NP 問題也可能在實務上來的比另一個 P 問題有效率， 例如 Knapsack Problem、Boolean Satisfiability Problem、Travelling Salesman Problem 等問題目前已經可以在可接受的時間內取得答案， 這些問題以平均複雜度來看可能會意外的低， 像是 Linear Programming 中的 Simplex 演算法雖然在最差複雜度上是指數成長的， 但它在實務上卻跑得和多項式時間演算法一樣好。

另外要注意的是， 有些計算方式並不符合 Turing Machine 的運作， 而 P 和 NP 問題是以 Turing Machine 為基礎在討論的， 因此如果換上了量子電腦這類不同的計算模型， 那這邊的討論就無法套用上去。

停機問題 (Halting Problem)

停機問題是指要做出一個程式可以判斷任意程式是否能在有限時間內執行完畢是不可能的， 類似命題還有理髮師悖論和全能悖論。

假設停機問題有解， 我們有一隻程式 H 可以判斷程式 P 在輸入資料 I 的狀況下是否會停（ H(P, I) ）， 那我們可以做出一隻程式如下：

if H(P, I) == STOP:
    infinite_loop()
else:
    stop()

也就是說這隻程式會在輸入資料會停止的狀況下進入無窮迴圈， 並且在輸入資料不會停止的狀況下停止， 也就是會跟輸入的資料行為相反， 但此時我們把這隻程式餵給自己， 也就變成：

if H(P, P) == STOP:
    infinite_loop()
else:
    stop()

不管怎樣現在這隻程式的行為都不會和判斷的結果相符， 因此前面假設我們存在「可以判斷任意程式是否會停止」的程式是不合理的。

書籍

參考